Warum habe ich diesen Artikel geschrieben? Ich möchte Ihnen eine anwendungsorientierte Einführung in die FEM Berechnung und ihren industriellen Einsatz zur Verfügung stellen.
In unserem ersten Blog-Artikel Digitaler Zwilling und Virtueller Prototyp in Industrie 4.0 – Simulation macht sie lebendig haben wir zunächst die Begriffe Digitaler Zwilling, Virtueller Prototyp und Simulationsmodell definiert.
Anschließend haben wir erklärt, warum Simulationsmodelle in der Produktentwicklung das Fundament für den Einsatz von Digitalen Zwillingen bilden.
In unserem zweiten Blog-Artikel Simulation in der Produktentwicklung – der schnelle Weg zu optimalen Produkten und Fertigungsprozessen haben wir gezeigt, welche Chancen und Herausforderungen der Einsatz von Simulation mit sich bringt.
Wenn es uns mit diesen Artikeln gelungen ist unsere Begeisterung für Simulation mit Ihnen zu teilen, haben Sie sich vielleicht schon gefragt:
Wie wird der Einsatz von Simulationsmodellen konkret in die Tat umgesetzt?
Um diese Frage zu beantworten, müssen wir den Begriff Simulation zunächst noch mit etwas mehr Leben füllen.
Um ein Simulationsmodell für eine konkrete Fragestellung aufzubauen, werden Simulationsmethoden und Simulationssoftware verwendet.
Je nachdem welche physikalische Fragestellung Sie primär beschäftigt benötigen Sie unterschiedliche Simulationsmethoden und eine passende Simulationssoftware für die praktische Umsetzung.
Wir werden uns in diesem Artikel zunächst mit einer der wichtigsten Simulationsmethoden im Maschinenbau widmen, der
Finite Elemente Methode.
Die Finite Elemente Methode (FEM) wird häufig auch als FEM Berechnung oder Finite Elemente Analyse (FEA) bezeichnet. Sie ist eine der meistverwendeten numerischen Simulationsmethoden.
Die FEM Berechnung kann zur Analyse von Fragestellungen aus der Strukturmechanik (Statik/Dynamik), der Wärmeübertragung und sogar zur Behandlung elektrischer bzw. elektormagnetischer Probleme verwendet werden. Beginnen wir mit der Frage:
Was kann die FEM Berechnung im Produktentwicklungsprozess für uns leisten?
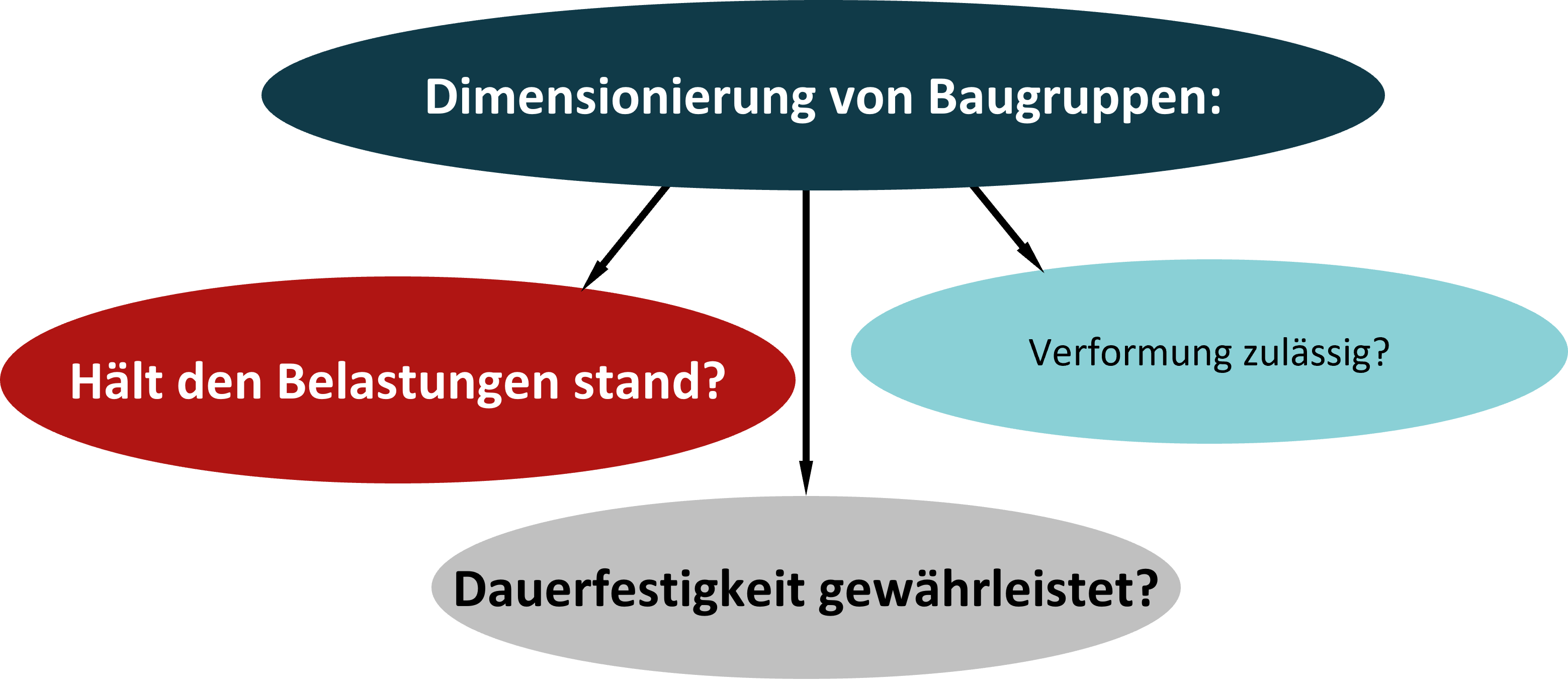
In der Produktentwicklung sind Baugruppen von Maschinen und Anlagen zu dimensionieren. Je nach Anwendung müssen hierfür unterschiedliche Fragen beantwortet werden. Für jede Baugruppe ist zu prüfen, ob sie den Belastungen standhält.
Bei dynamischen Belastungen ist, abhängig von den Lastkollektiven, die Betriebs- oder Dauerfestigkeit sicherzustellen.
Wenn die Verformungen im Sinne der Funktion bestimmte Grenzwerte nicht überschreiten dürfen (z.B. Wellen, Kräne, Brücken) muss dies zusätzlich geprüft werden.
All diese Fragen lassen sich für beliebig komplexe Baugruppen und Maschinen mit der FEM Berechnung beantworten.
Statt mit trockener Theorie wollen wir Ihnen die FEM an einem konkreten Beispiel vorstellen. Als Anwendungsbeispiel haben wir hierfür einen auskragenden Träger, der mittels einer angeschweißten Platte an eine Wand angeschraubt wird, ausgewählt.
Nachfolgendes Bild zeigt das Verformungsfeld des zugehörigen Simulationsmodells, welches mit der FEM Berechnung ermittelt wurde. Hierfür wurde die Open-Source-Simulationsumgebung Salome-Meca mit dem integrierten FEM-Solver Code_Aster verwendet.
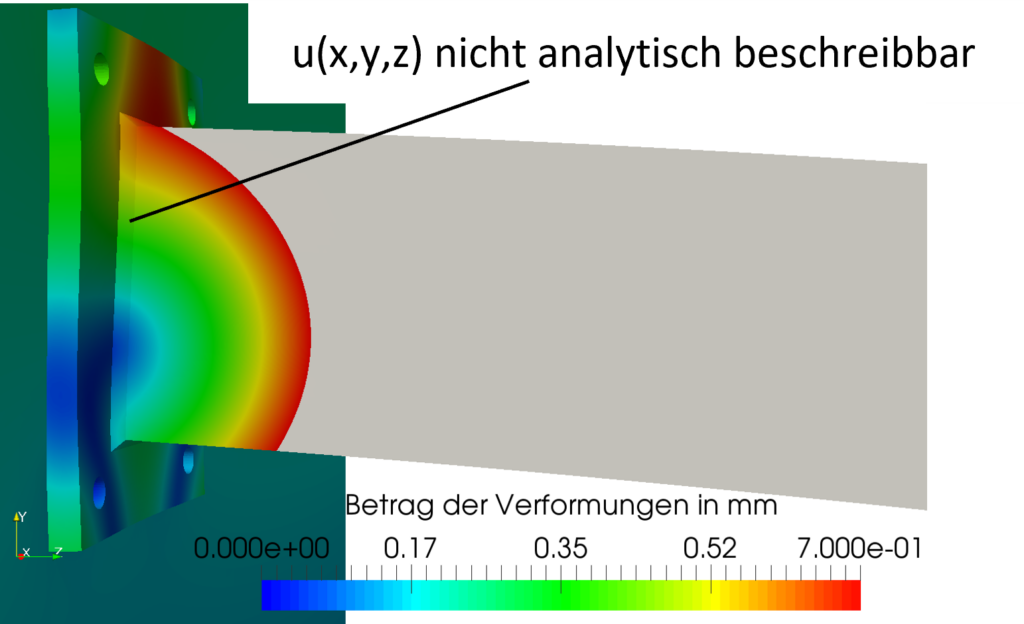
Die Verformungen u(x,y,z) werden auf der Oberfläche des Biegebalkens dargestellt und erlauben dem Betrachter eine anschauliche Zuordnung der Werte u zu den Positionen (x,y,z) auf dem Balken.
Verläufe von Verformungen, Spannungen, Temperaturen usw. sind typische Ergebnisse von FEM Berechnungen. Es handelt sich hierbei um sog. ortsabhängige Feldgrößen. Die oben gezeigte Art der Darstellung von Feldgrößen wird als Konturplot bezeichnet.
Noch ein Effekt wird sichtbar: Die FEM Berechnung ist ein Werkzeug, um den Verlauf physikalischer Größen an nahezu beliebig geformten Bauteilen zu berechnen. Häufig sind komplexere Geometrien als der dargestellte Träger zu behandeln.
Sogar im hier vorliegenden Beispiel können mit der „Handrechnung“ (z.B. Kragbalkenformel) nur die Nennspannungen im Anschluss berechnet werden und nicht die lokalen Spannungs-Peaks in der Schweißnaht.
FEM Berechnung – von der Differentialgleichung zum praktischen Ergebnis
Physikalische Zusammenhänge werden in Differentialgleichungen formuliert, wie für eine Platte unter gleichförmig verteiltem Druck
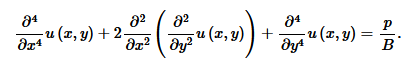
Die Frage ist, wie wir diese Differentialgleichungen lösen. Denn die gesuchte Größe ist das Verformungsfeld u(x,y).
In den Differentialgleichungen stehen Ableitungen dieser Feldgröße. Wir können die Gleichung also nicht einfach nach der gesuchten Größe umstellen.
Die Lösung ist mathematisch nicht einfach, weil wir eine zur Geometrie passende Ansatzfunktion benötigen.
Diese zu finden, wird immer schwerer, je komplexer die Geometrie ist. Somit wird die Lösung für komplexe Geometrien auf diesem Weg schwer bis unmöglich.
Für einfache Geometrien, wie Dreiecke und Tetraeder, finden wir problemlos Ansatzfunktionen und die Differentialgleichungen wird lösbar.
Baut man eine Struktur aus diesen Geometrien, den Finiten Elementen, auf (das nennt man Diskretisierung oder Vernetzen) und fügt sie an den Knoten mathematisch zusammen, entsteht ein großes lineares Gleichungssystem.
Durch die Diskretisierung wandeln wir also komplexe Differentialgleichungen in eine größere Menge gewöhnlicher linearer Gleichungen um.
So erhalten wir oft sehr große lineare Gleichungssysteme die problemlos durch Computer gelöst werden können. Wir verringern so die Komplexität, erhöhen aber den Arbeitsaufwand.
Das ist aber kein Problem, weil diese einfache Arbeit problemlos ein Rechner für uns erledigen kann. Wir müssen nur noch warten.
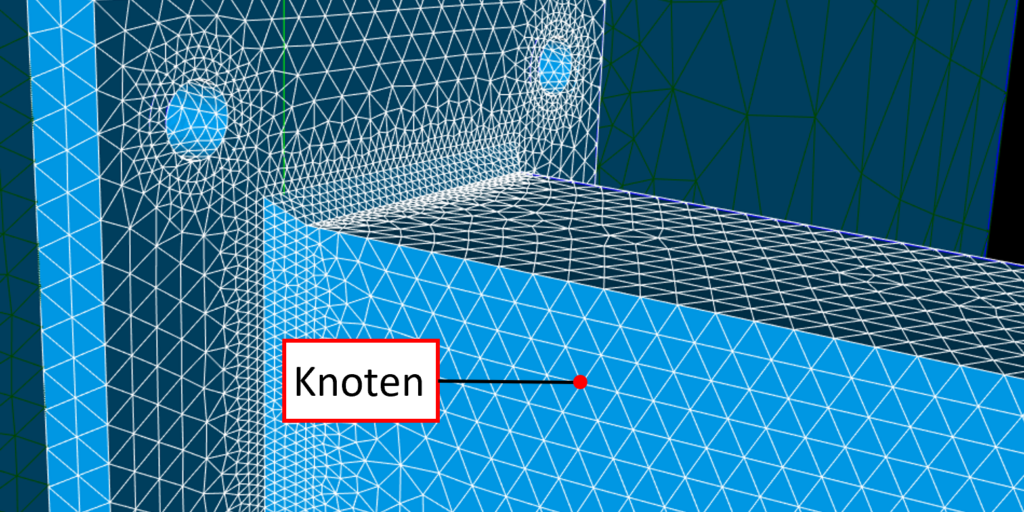
Als Ergebnis liefert die FEM Berechnung uns die Verläufe verschiedenster physikalischer Feldgrößen, wie Spannungen und Verformungen, über die vernetzte Struktur.
Dieser Verlauf verrät weit mehr über das Geschehen in der Struktur, als es durch Messungen an realen Prototypen möglich wäre.
Messungen liefern nur Einzelwerte an ausgesuchten Messstellen.
Die Anzahl der Messstellen ist i.d.R. über das verfügbare Budget für die Messtechnik begrenzt.
Ein weiterer Nachteil des Messens ist, dass offen bleibt, was zwischen den Messstellen passiert.
Die Messung ist allerdings eine hervorragende Möglichkeit, um Simulationsmodelle an einzelnen Stellen zu validieren. Die große Bandbreite der Erkenntnisse liefert dann oft das Simulationsmodell.
Ablauf einer FEM Berechnung
Eine FEM Berechnung besteht aus drei Arbeitsbereichen:
- Aufbau des Simulationsmodells (Präprozessing),
- Rechenlauf und
- Auswertung (Postprozessing).
Es kann sich eine Optimierung anschließen, die wir zur Vereinfachung nicht betrachten.
Der Aufbau des Simulationsmodells erfolgt schrittweise.
Zuerst wird die Geometrie erstellt oder aus einem CAD-Programm übernommen und es werden alle erforderlichen Definitionen, z.B. für das Aufbringen von Belastungen, durchgeführt.
Nachfolgende Abbildung zeigt ein Beispiel dieses Präprozessings in Salome-Meca.
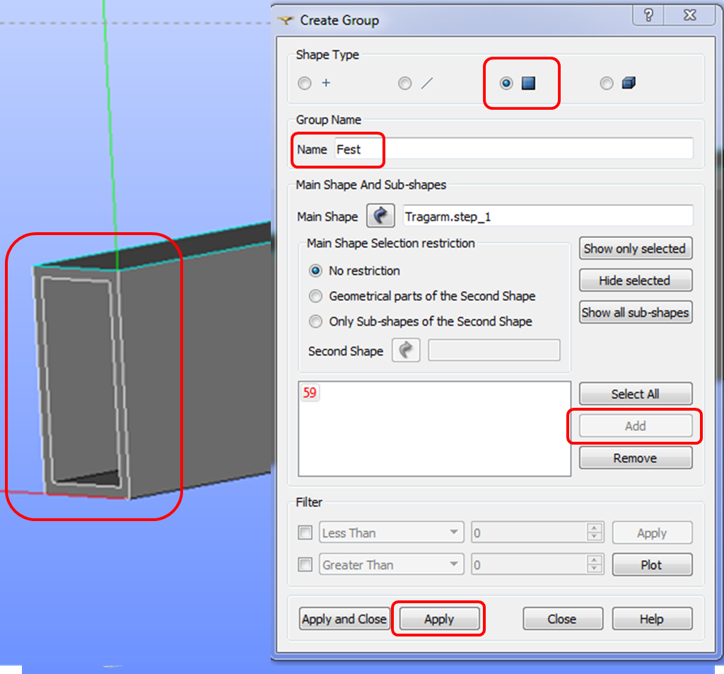
Anschließend wird die so erstellte Geometrie mit Finiten Elementen vernetzt. Funktionen für die Netzgenerierung nehmen dem Anwender die meiste Arbeit ab.
Die Finite-Elemente-Methode liefert eine Näherungslösung deren Abbildungsgüte von der Netzgenerierung abhängt. Es gibt immer eine Abweichung vom realen Verlauf der betrachteten physikalischen Größen. Sie wird auch als Abbildungsgüte bezeichnet und kann durch die lokale Verfeinerung des Netzes verbessert werden.
Ist die Netzgenerierung abgeschlossen, werden die Verschiebungsrandbedingungen und die Lasten definiert.
Zu unterscheiden ist zwischen:
- Festhaltungen,
- Einzellasten und Drücken
- Klebekontakten,
- Couplings und
- nichtlinearen Kontakten.
Festhaltungen blockieren alle Freiheitsgrade eines Knotens (ui = 0). Damit wird eine unendliche Steifigkeit modelliert, die so in der Realität nicht vorkommt. Um unphysikalische Effekte zu vermeiden, müssen Festhaltungen mit Bedacht eingesetzt werden.
Ähnliches gilt für die Kopplung von einer Gruppe von Knoten mit der Starrkörperbewegung eines Referenzknotens (Coupling). Bei Klebekontakten, also der Verbindung von Knoten unterschiedlicher Elemente, erfahren die verbundenen Knoten dieselbe Verschiebung.
Können die Oberflächen von in Kontakt befindlichen Bauteilen sich unter Belastung voneinander lösen, wie es bei Schraubverbindungen und Wälzlagern der Fall ist, werden nichtlineare Kontakte eingesetzt.
Im Zuge der Modelldefinition folgen die Auswahl eines passenden Materialgesetzes und die Eingabe der zugehörigen Parameter, wie E-Modul und Querkontraktionszahl.
Hinzu kommen die nötigen Angaben für den Lauf des FEM-Gleichungslösers, wie Anzahl der zu nutzenden Prozessoren und Konvergenzkriterien.
Schließlich muss noch festgelegt werden, welche Größen in die Ergebnisdateien der FEM Berechnung auszugeben sind.
Das können
- Verschiebungen,
- Verzerrungen,
- Spannungen,
- Vergleichsspannungen,
- Temperaturen
und viele andere Werte sein, die in der Struktur feldartig verteilt sind.
Verschiedene Bereiche der Physik in der FEM Berechnung nutzen
Jede FEM Software unterstützt verschiedene Bereiche der Physik, wie Statik und Dynamik in der Festkörpermechanik, Thermodynamik, Bruchmechanik und Wechselwirkungen, wie Fluid-Struktur-Interaktion. Neben grundlegenden Funktionen werden häufig eigene Module angeboten, die ausgewählte Teilbereiche der Physik unterstützen.
Über interne und externe Kopplungen können mehrere physikalische Domänen in einer FEM Berechnung zusammenwirken. Anwendungen der Thermo-Hydro-Mechanik und Fluid-Struktur-Interaktionen sind eindrucksvolle Beispiele hierfür.
Die Kopplung verschiedener physikalischer Domänen kann innerhalb eines FEM Programmes erfolgen. Sind die nötigen Schnittstellen vorhanden, können auch verschiedene Simulationssoftware-Tools für eine gekoppelte Analyse eingesetzt werden.
So werden für eine Fluid-Struktur-Interaktion oft die FEM- und CFD-Solver unterschiedliche Softwarepakete gekoppelt
Die FEM Berechnung bietet unschlagbare Vorteile im Maschinenbau
Der Einsatz der FEM Berechnung in der Produktentwicklung hat viele praktische Vorteile, von denen wir hier einige erörtern. Die größten Vorteile liegen häufig in der Einsparung von Kosten und Zeit.
Ein großer Teil der Kosteneinsparung ergibt sich, wenn reale Prototypen teilweise oder ganz eingespart werden können. Am Ende dieses Artikels liefern wir Ihnen hierzu noch ein einfaches Zahlenbeispiel.
Die FEM Berechnung gehört im Ingenieurwesen zu den meistverwendeten numerischen Methoden.
Deshalb sind viele Artikel, Berichte, Beispielrechnungen und Kontakte in Internetforen dazu verfügbar. Materialmodelle für häufig eingesetzten Werkstoffe, wie Stahl, Aluminium und Faserverbundwerkstoffe ermöglichen Vergleichsrechnungen mit dem Ziel der Materialeinsparung, des Leichtbaues und der Verringerung der Umweltbelastung.
Simulationen mit der FEM Berechnung bieten viel mehr Informationsgehalt als Messergebnisse.
Dadurch entsteht eine neue, weit umfangreichere Basis für Ideen und die Produktoptimierung. Dieser Punkt sollte nicht unterschätzt werden, weil er hilft, im Wettbewerb wichtige Vorteile durch Innovationen zu sichern.
Die Rechenergebnisse werden als Verläufe im berechneten Bauteil ermittelt. Der Erkenntnisgewinn ist nicht nur punktuell, wie bei einem Messwert.
Die FEM Berechnung ermöglicht die isolierte Betrachtung einzelner Bauteile mittels äquivalenter Randbedingungen.
Es muss nicht das ganze System gebaut werden, wie bei einem realen Prototyp, um einzelne Komponenten zu testen. Die fehlenden Bauteile können mit Randbedingungen simuliert werden.
Im Simulationsmodell können physikalische Gesetze nach Bedarf ein- und ausgeschaltet werden. Der Anwender gewinnt genaue Erkenntnisse über die Einflussgrößen.
Auch in der Anwendung der FEM Berechnung wächst die Flexibilität. Liegt das FEM-Modell vor, kann es für verschiedene Simulationen eingesetzt werden.
An einem realen Prototyp müsste dagegen jedesmal der Versuchsaufbau geändert werden.
Oft ist der Raum für die Anbringung und Verkabelung von Sensoren an einem Maschinenbauteil nicht gegeben oder die Notwendigkeit dafür wird erst nach dem Zusammenbau erkannt. In diesen Fällen spart FEM-Simulation viel Zeit und Geld.
Hohe Realitätsnähe durch nichtlineare FEM Berechnung
Zur Steigerung der Realitätsnähe einer FEM Berechnung können Nichtlinearitäten berücksichtigt werden. Es werden drei Arten von nichtlinearen Effekten unterschieden:
- nichtlineare Kinematikmodelle (große Verformungen),
- nichtlineares Materialverhalten,
- nichtlinearer Kontakt.
Bei den nichtlinearen Verformungen sind die großen Rotationen von besonderem Interesse.
Für die Abbildung von nichtlinearem Materialverhalten existieren zahlreiche Stoffgesetze für nichtlineare Elastizität, Plastizität, Anisotropie, Temperaturabhängigkeit der Stoffwerte usw.
Mit nichtlinearem Kontakt kann die Berührung und Ablösung von Bauteilen, d.h. Strukturvariabilität, untersucht werden.
Auch die Veränderung einer Kontaktfläche bei Erhöhung der Anpresskraft (Hertzsche Pressung) lässt sich mit dem nichtlinearen Kontakt im Unterschied zum linearen Kontakt, auch als Klebekontakt bezeichnet, darstellen.
Kostensenkung mit FEM Berechnung
Vor der Einführung von FEM Berechnung ist es hilfreich, Rechenschaft über die bisherige Vorgehensweise abzulegen. In vielen Unternehmen werden noch heute reale Prototypen eingesetzt, um Funktion und Belastbarkeit der Produkte sicherzustellen.
Nicht selten wird dafür ein intuitives Try & Error-Verfahren angewendet. Den Beteiligten ist oft nicht bewusst, dass es sich so lange um einen realen Prototyp handelt, bis alles funktioniert. Das gilt auch für den Bau eines Einzelstückes, wie einer Sondermaschine.
Der Preis ist, dass die Produkte häufig überdimensioniert und unnötig teuer in der Herstellung sind. Würde stattdessen von Anfang an ein Virtueller Prototyp mit Simulation genutzt, könnten auch bei geringen Stückzahlen hohe Potenziale für Kosteneinsparung und Qualitätserhöhung abgeschöpft werden.
Gleichzeitig steigt die Termintreue und die Belastung für die Mitarbeiter sinkt. Wie so oft im Leben ist auch hier alles eine Frage der Konsequenz.
Zahlenbeispiel für Kostensenkung
Die positive Veränderung gegenüber der konventionellen Vorgehensweise lässt sich in Zahlen leicht abschätzen. Betrachten wir dafür ein einfaches Beispiel.
Die Kosten für einen Prototyp liegen typischerweise im 4- oder 5-stelligen Bereich. Gehen wir zunächst vereinfachend davon aus, dass die realen Prototypen komplett eingespart werden. Sind normalerweise 10 reale Prototypen mit Kosten von je 5.000 Euro pro Jahr zu fertigen, ergeben sich hierfür Kosten von
10 x 5.000,- € = 50.000,- €.
Die Einsparungen, welche mit der FEM Berechnung zu erreichen sind, lassen sich so einfach ausrechnen.
Werden durch den Einsatz der FEM Berechnung alle realen Prototypen eingespart, ergeben sich Kostensenkungen von bis zu 50.000,- €.
50.000 EUR Einsparung in einem Jahr sind ein üppiges Budget um eine eigene Simulationsstrategie zu entwickeln und das nötige Simulations-Know-How aufzubauen.
Diese Rechnung wird nach unserer Erfahrung in Unternehmen selten gemacht. Hier liegt viel verschenktes Geld und viel Potenzial für leicht verdiente Wettbewerbsvorteile.
Wird eine FEM Freeware (Open-Source-Software) für die FEM Berechnung genutzt, ergibt sich zusätzlich ein hoher wirtschaftlicher Vorteil gegenüber Unternehmen, die kommerzielle Simulationsoftware einsetzen.
Schließlich müssen diese Unternehmen die jährlichen Lizenzkosten auf ihre Kundenprojekte umlegen.
In meinem Artikel „Entwicklungskosten mit Simulation um 90% senken“ finden Sie eine ausführlichere Berechnung der möglichen Kostenersparnisse anhand eines konkreten Fallbeispiels.
Anwendungsbeispiel Festigkeitsberechnung einer Halterung mit der FEM Berechnung
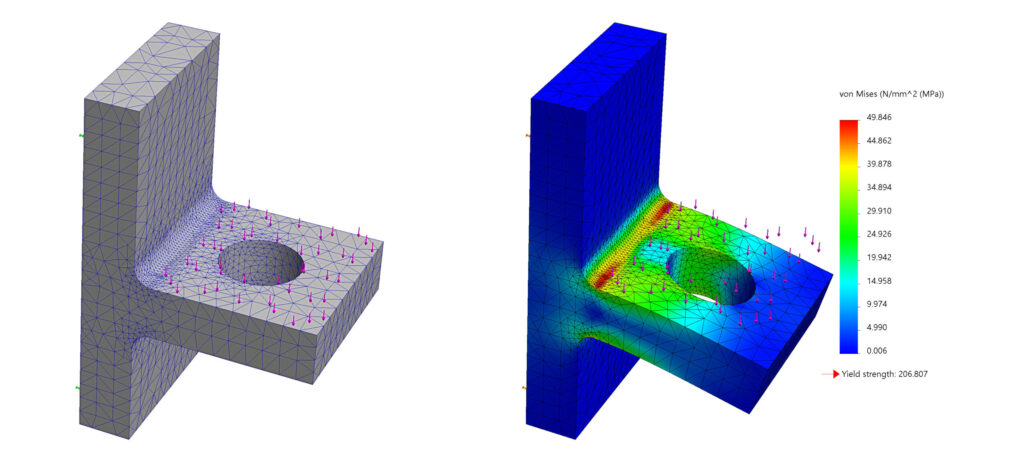
Nachfolgend sehen Sie das diskretisierte Simulationsmodell (links) und den Konturplot der von-Mises-Vergleichsspannungen für eine einfache Festigkeitsberechnung eines Halters.
Es wird deutlich, dass die maximalen Spannungen (50 N/mm²) weit unterhalb der Fließgrenze (207 N/mm²) des verwendeten Materials liegen. Es ergibt sich eine Sicherheit von ca. 4 gegen Fließen.
Wir würden sagen: Hier kann ruhig noch etwas Material eingespart und optimiert werden. Gerade wenn es sich um ein Serienteil handelt, ist dies äußerst lohnenswert.
Haben Sie noch Fragen zur FEM Berechnung oder gibt es noch Unklarheiten? Setzen Sie die Finite Elemente Analyse bereits in Ihrem Unternehmen ein? Hat unser Artikel Ihr Interesse am Einsatz von Simulationsmodellen geweckt? Ich freue mich auf Ihre Fragen und Ihr Feedback in den Kommentaren.



0 Kommentare